타입 시스템.
실행되서는 안되는 프로그램들
프로그램을 만드는 방법을 충실히 따라서 제대로 생긴 프로그램을 만드는 것은 쉽습니다. 그런데, 그 중에는 실행될 수 없는 프로그램들이 많습니다.
(프로그램이라고 표현했지만, 좀 규모를 축소하면 코드라고 표현 하는게 프로그래머에게 더 와닫겠군요.)
실행되서 어떤 루틴에서 동작하지 않는 프로그램, 메모리를 과도하게 사용하여 시스템을 멈추게 하는 프로그램, 무한 루프에 빠진 프로그램.... 등등.
예를 들지 않아도 아마 대충은 감이 올것입니다.
실행되서는 안되는 이라고 했지만, 좀더 평범하게 표현하자면, 실행되지만 잘 돌지 않는 프로그램이라고 표현하는 것이 좋겠네요.
프로그램을 만드는 방법( 문법) 적으로는 문제가 없지만, 실제로 동작했을때 제대로 실행되지 않는 프로그램들이 있습니다.
사용자들은 제대로 동작하는 프로그램들을 동작시키길 원하고, 이런 프로그램들을 미리 확인하고 싶어합니다.
컴퓨터 사이언스에서는 이런 프로그램들을 찾고 검증하는 기술들이 점점 발전하고 있습니다.( 물론 완전한 프로그램은 없습니다... Halt problem ...)
다른 분야들에서는(기계설계, 건축 등) 인공물들이 자연세계에서 문제 없이 동작할 지를 미리 분석하는 수학적 기술들이 잘 발달해 있습니다.
뉴튼 역학, 미적분 방정식, 통계 역학 등등.
소프트웨어 분야에서는 아직 완전한 기술들은 없지만, 최종 목표는 소프트웨어가 오류없이 작동할 지를 실행전에 자동으로 검증하는 기술을 이룩하는 것입니다.
이 축을 따라 프로그래밍 언어에서 , 프로그래밍 언어가 어떻게 디자인 되면 이문제가 어디까지 해결될 수 있을까? 프로그래밍 언어 분야에서는 이 시급한 문제에 어떤 답을 내 놓고 있는가?
현재 어느 정도 수준인가?
프로그래밍 언어 분야를 돌이켜 보면, 다음과 같은 단계를 거치면서 한발짝을 나아가고 있습니다.
1. 우리가 확인 할 수 있는 오류의 한계를 정확하게 정의한다.
2. 정의한 오류의 존재를 찾는 방법을 고안한다.
3. 컴퓨터가 자동으로 실행할 수 있도록 소프트웨어를 만든다.
각 단계별로 애매하고 허술한 구석이 없을때에만 비로소 한 발짝의 전진이 있게 됩니다. 이 단계들이 반복되면서 소프트웨어의 오류의 정의는 점점 정교해집니다.
현재 이렇게 해서 발전된 단계는 겨우 두발자국 이라고 합니다.
1세대 기술 : 문법 검증 기술
1970년대에 달성된 첫 발짝은 ,생긴게 잘못된 프로그램을 찾아내는 기술입니다.
이 기술은 안전하고 빠뜨림 없이 문법이 오류인 것을 찾아주는 것을 의미합니다.( 새로운 것이 아니라 이미 우리는 이렇게 코딩하면서 컴파일러를 통해서 오류들을 찾아내고 있습니다.)
그러나, 여전히 제대로 동작하지 않는 프로그램을 찾아 내지는 못합니다.
2세대 기술 : 타입 검증 기술
1990년대에 빛을 보기시작한 기술입니다.
이때의 오류의 정의튼 겉모양이 틀린 프로그램 외에 속 내용이 잘못되어있을 수 있는 경우를 포함합니다.
프로그램 실행은 일종의 계산인데, 계산중에는 분별있는 일들이 일어납니다.
더하기에 숫자만 들어와야 한다. 수력발전하기 에는 물이 들어와야 한다. 햄버거 만들기에는 퍼티와 빵이 들어와야 한다...
등등의 분별력있는 계산식과 그에 맞는 데이타가 필요한데, 그렇지 않는 경우들이 발생되면, 프로그램은 생각대로 동작하지 않습니다.
타입이 맞지 않는 계산이 실행중에 발생할지를 미리 검증하는 방법이 타입검증입니다. 프로그램의 안전한 타입검증은 그 프로그래밍 언어가 제대로 디자인된 경우에만 가능합니다.(ML, OCaml, Haskell)
프로그램 E의 문법 규칙을 다음과 같다고 하자.
이 때 2+"a" 는 문법 규칙에는 맞습니다. 하지만 프로그램의 흐름상 잘 동작하리라는 보장은 못합니다.
우리는 + 식에 대해서 두개의 부품식은 모두 정수여야 한다는 규칙이 필요합니다.
하지만, 문법 규칙에는 대개 표현하지 않습니다.
이런 문법을 표현하게 되면, 우리는 "문법규칙" 의 영역에서 "타입 시스템"의 영역으로 은근 슬쩍 넘어가게 됩니다.
"x+1"이 말이 되려면, x는 정수여야 합니다. 텍스트가 가지는 속 내용을 문맥으로 고려해야 합니다.
우선 이를 해결하기 위해서 타입시스템을 만들어봅시다.( 실제로 이미 만들어진 시스템을 학습하는 차원에서 한발 한발 나아가는 것입니다.)
우선 실행중에 위에서 x가 정수인지 아닌지 판단하는 것을 실행기(interpreter)에서 구현했다면, 이를 동적 타입 검증 (dynamic type checking)이라고합니다.
덧셈 "E1+E2"의 두식이 "+" 연산을 하는 시점에 E1이나 E2가 정수가 아닌지 판별하려면, E1식의 결과가 정수이어야 하고, E2의 결과가 정수이어야 합니다.
"+" 연산 시점에서 비로소 판단 할 수 있는 것입니다.
쉽게 만들어지겠죠.?
그러나 우리에게 필요한 것은 정적 타입 검증(static type checking) 입니다. 프로그램 실행전에 타입을 검증하기
즉, 문제를 미리 찾아내고 무결점임을 확인한 후에 실행을 시작하는 것이 필요합니다.
여러번 언급했던것 처럼 오류를 완전하게 찾아내는 시스템은 만들 수 없습니다. 그렇기 때문에 믿을만한, 안전한, Sound한 시스템 이었으면 합니다.
타입 검증 시스템이 문제 없을 것이라고 했는데 실행중에 문제가 발생하는 경우가 없었으면 좋겠다는 것입니다.
Type
우리가 정의한 언어에는 계산하는 값들의 종류가 5가지입니다.
다음 과정을 통해 type을 정의해봅니다.
1. 기본 값(primitive value)의 종류마다 이름을 붙입니다.
2. 레코드 는 복합 값입니다. 레코드의 부품들로 만들어진 복합타입을 갖습니다. (compound value,compound type)
3. 메모리 주소는 값을 보관하고 있고, 메모리주소의 타입은 보환하고 있는 값의 타입에 따라 분류한 복합 타입입니다.
4. 프로시져는 값은 아니지만 그 타입을 가지고 호출식들이 제대로 쓰이는 지 확인할 필요가 있습니다.
타입검증 규칙
을 증명하는 논리 규칙들은 다음과 같습니다.
T(Gamma)는 프로그램에 나타나는 이름들의 타입을 가진 테이블입니다.
:
:
재미있는 사실은 이 타입 시스템은 프로그래머가 타입에 대해서 프로그램 텍스트 안에 써 넣은 것이 전혀 없습니다.
(우리는 실제로 이런 언어가 있다는 것도 알고 있습니다.)
이 타입 시스템을 보면, 프로그램의 구석구석이 어떤 타입을 갖는다고 판단 될 수 있는지 순수하게 논리 시스템으로 바라보자.
이 시스템은 그럴듯 하지만 아쉬운 면이 있습니다. 안전(sound)하지도 완전(complete)하지도 않습니다. 이 두가지 문제를 자세히 다루겠습니다.
안전하지 않다.
타입시스템이 문제없다고 판단한 프로그램이 실행중에 타입 오류로 멈출 수 있습니다.
type 리스트 = {int x, 리스트 next }
let
리스트 node = {x:=1, next:={}}
in
node.next.x
end
위와 같은 프로그래밍은 C나 C++에서 흔히 보는 경우입니다.
typedef struct _OT
{
int x;
struct _OT * pNext;
}OTStruct;
int getNextVal(OTStruct* pOt)
{
return pOt->pNext->x; //<-- 이 부분이 정상 수행되기 위해서는 여러가지 채크가 필요합니다. 그래야 정상으로 동작하죠.
}
"상식 수준에서 " 키워온 우리 언어에서는 해결할 수 없습니다. 언어를 다지아니 할 때 부터, 이 문제를 염두에 두고 잘 디자인 해 가야 해결 할 수 있는 문제입니다.
(C나 C++등 초창기에 만들어진 언어들에서는 알려지지 않은 오류들이었을 것입니다. 그래서 그 당시에는 이런 문제가 있을 것이라는 예상이 불가능 했을 것이고 말이죠. )
안전하게 되기 위해서 지금까지 설명했던 우리의 언어는 제 정의될 필요가 있습니다. 더이상 이전의 언어는 아닐 것입니다.
안전한 타입 시스템을 고안하고 구현할 수 있게 된다면, 그 타입 시스템을 통과하는 프로그램은 매우 소수가 될 것입니다.
그런 프로그램은 제한된 기능만 가지고 작성된 프로그램들이 도리것입니다.
또, 안전하게 되기 위해서 매우 정교한 타입 시스템을 고안하게 될것이고, 그 정교함이 극에 달해서 아마도 지금의 기계로는 구현할 수 없는 것이 될것입니다.
어떻게 실용적인 범용의 언어가 이 문제를 해결한 편리한 타입시스템을 갖추게 되었는지 는 값 중심의 언어에서 다루게 될것입니다.
그 전에 좀더 타입에 대해서 다뤄볼 필요가 있습니다.(두번째 문제점을 다룰 차례죠)
완전하지 않다.
제대로 도는 프로그램중에서 위의 타입 시스템을 통과하는 것은 일부분 입니다.
제대로 잘 도는 프로그램도 타입이 없다고 판단할 수 있습니다.
let x:=1
in x:=true
>> reject !!
let procedure f(x) = x
in
f(1); f(true)
// reject!!
let procedure f(x)= x.age:=19
in f ( {age:=1, id:=001});
f ( {age:=2, height:=170})
//reject !!!!
1. 메모리 주소의 타입이 변할 수 가없다.
메모리 주소에 처음으로 보관되는 초기값의 타입이 그 주소가 저장할 수 있는 값들의 타입으로 고정됩니다.
2. 어떤 프로시져는 인자값의 타입에 상관없이 실행될 수 있는 프로시져 들이 있다.
이러한 프로시져는 다양한 타입의 인자를 받으면서 아무 문제 없이 실행될 수 있습니다.
그러나 이 타입 시스템은 통과 할 수 없습니다.
3. 레코드 타입 관련해서도 타입 검증이 너무 까다롭다.
복합적인 데이타를 표현하는 데 쓰이는 레코드의 타입이 유연하지 않습니다.
리스트를 예로 들어보면,
lst :={val:=0,next:={}};
lst.next:= {val:=100,next:={}};
lst의 next 는 빈 레코드 타입으로 고정될 수 없습니다.초기에는 빈 레코드이지만 다음 라인에서 다른 레코드로 변경되어 버렸습니다.
즉, static하게 next의 타입을 판단 할 수 없다는 의미가 됩니다.
이 문제는 타입의 안정성을 개의치 않는다면 쉽게 해결 방법이 나옵니다. (대부분의 현재 언어들이 취하고 있는 방법입니다.)
프로그래머가 타입을 정의하고 이름을 지을 수 있도록 합니다.
그리고 그 이름이 타입 정의에서 재귀적으로 사용될 수 있도록 합니다.
type list = {int val, list next}
이렇게 정수를 가지는 val 필드와 재귀적으로 list를 품을 수 있는 next 필드로 표현하고, 리스트의 깊이는 표현할 필요가 없습니다.
1. 타입 이름들의 유효범위는 프로그램전체가 되도록 하였습니다.
2. 타입 이름들이 정의 되는 곳은 프로그램의 처음 부분 뿐입니다.
빈 레코드의 식은 임의의 타입으로 결정될 수 있다고 타입 규칙으로 정의합니다.
대신
로, 빈 레코드를 초기에 가지게 되는 리스트 레코드의 next 필드는 list타입이 되는 것으로 판단 되는 것이다.
lst :={val:=0,next:={}};
lst.next:= {val:=100,next:={}};
lst의 타입은 list loc으로 판단할 수 있고, 두번째 줄의 지정문도 타입 검증을 통과합니다. lst.next 도 list loc 이기 때문입니다.
여기서 중요한 아이디어는 이름을 사용한다는 것입니다. 타입에 이름을 붙이고 그 이름으로 속 내용을 감춥니다.
재귀적인 구조를 구현하는 레코드는 재귀 고리 역할을 하는 필드가 있습니다.
임의의 깊이로 레코드를 품을 수 있는 필드의 타입을 사용해야 하지만 이를 표현하지 않기 위해서 이름을 사용하는 것입니다.
이 해결책 역시 어설픈 이유는, 타입 시스템이 안전하지 않은 문제가 해결되지 않았기 때문입니다.
안전성을 포기하고 이렇게 고안된 방법들이 현재 대부분의 프로그래밍 언어에 적용되었습니다.
자! 다시 좀더 깐깐하게 짚어보면, 위의 타입시스템으로 작성된 프로그램의 구석 구석 타입이 제대로 되었는지 증명해 낼 수 있을까?
타입 규칙들은 의미규칙과 다른 양상이 있습니다. 타입 검증기 구현은 의미규칙을 보고 실행기를 구현할 때와 같이 간단하지 않습니다.
이 구현의 문제를 간단히 넘어가는 방법(선택의 여지가 없었는지도 모른다)은 프로그래머가 타입 검증을 돕는 코맨트를 프로그램 택스트에 포함시키도록 강제하는 것입니다.
C,C++,Pascal, Java 등의 언어가 이런 방식으로 구성되어있습니다.
의 증명을 구현하는 타입 검증 함수의 입력은 두가지가 될것입니다. 프로그램 식 E와 T(Gamma).
주어진 두개의 입력에 대해서 타입 검증 함수는 위의 타입 판단에 해당하는 r(tau)가 있는지를 찾게 됩니다.
타입 환경 T는 프로그램에 나타나는 이름들의 타입들에 대해서 알려진(가정) 내용입니다.
이것을 가지고 프로그램 텍스트 E가 타입 r를 가질 수 있는지 타입 규칙에 준해서 알아보는 것입니다.
프로그램 전체에 대해서는 시작 T는 물론 비어있을 것입니다. 타입 검증 함수가 프로그램의 부분들에 대해서 재귀적으로 호출되면서 T에 정보가 쌓이게 됩니다.
우리의 타입시스템에서 구현이 어려운 이유는 다음 규칙에서 드러납니다.
타입 검증에서 함수에 입력으로 줄 타입환경
은 이미 우리가 알아내야할 r1과 r2가 사용되고 있습니다. 그 두 타입들이 프로시져의 타입을 구성하기 때문입니다.
출력으로 알아내야 할 것을 입력으로 넣어 주어야 하는 것입니다.
이렇게 x의 E1의 타입을 프로시져에서 명시적으로 주면 간편해 집니다.
지금까지의 내용을 종합해서 프로그래머가 타입을 프로그램 코드( 택스트) 에 포함시키도록하자.
프로시저와 변수의 타입을 프로그래머가 명시하도록 하는 것입니다.
이 문법으로 프로그래밍을 하면 다음과 같습니다. 그리고 타입 검증이 통과 할 것입니다.
e.g.)
type bbs = { int name, bool zap }
let bbs x:={ name:=0, zap:=true }
in
if x.zap then 1
else x.name
e.g.)
type intlist = { int x, intlist next }
let inlist l := { x:=0, name:={} }
in
l.next :={ x:=1, next:={} }
l.next.next := { x:=1, next:={} }
e.g.)
type inttree = { inttree l, int x, inttree r }
let procedure shake( inttree t):inttree
= if t={} then t
else
let inttree t':={}
in
t':= call shake(t.l);
t.l : = call shake(t.r);
t.r:= t'
in
call shake( {
l:={},
x:=1,
r:={
l:={},
x:=2,
r:={}
}
} )
타입 환경(type environment)이 이전에는 프로그램에 나타나는 이름들 (변수, 프로시져 이름, 레코드 필드)의 타입에 관한 것이었으나, 이제부터는 타입 이름들의 속 내용(타입)에 대한 환경도 필요해 집니다.
타입에 대해서 다른 두가지 이슈가 더있는데 이부분에 대해서 간단히 언급하겠습니다.
우선 이름 공간(namespace)와 같은 타입 (type equivalence)에 대한 내용입니다.
우리 언어에서는 많은 것에 이름을 지을 수 있습니다. 메모리 주소(변수), 레코드의 필드, 플그램코드(프로시져), 타입에 이름을 정할 수 있었습니다.
타입 이름은 프로그램 전체가 유효범위 였고, 변수 이름과 프로시져 이름은 유효범위를 한정할 수 있었습니다.
같은 이름으로 타입 이름이나 변수 이름으로 사용해도 프로그램 텍스트에서 문제 없이 구분 할 수 있었습니다.
타입 이름과 메모리 주서의 이름은 다른 이름 공간을 가지고 있다고 예기 할 수 있고, 프로시저 이름 과 변수 이름은 같은 이름 공간을 공유합니다.
같은 타입이란 무엇인가?
type a= {int x; int y}
type b= {int y; int x}
내용이 같더라도 위와 같이 이름이 다르면 다른 타입인 것으로 정의(name equivence) 할 수도 있고, 내용만 같다면 같은 타입으로 정의(structural equivalence)할 수 도 있습니다.
우리의 언어에서는 타입 이름이 같아야 같은 타입인 것으로 정의한 셈입니다.
여기까지 해서 기계중심의 언어, 즉 상식선에서 프로그래밍 언어를 디자인 했던 과정을 따라가 보았습니다. 현재 널리 쓰이고 있는 명령형 프로그래밍 언어들이 만들어진 과정이기도합니다.
그 대표적인 언어가 C 언어 입니다. 어떻게 프로그래밍 언어를 디자인해야 하는지, 무엇이 문제일지가 드러나지 않은 상태에서 , 주어진 디지털 컴퓨터를 편하게 사용하기 위한 도구로서 프로그래밍 언어를 디자인 했던 과거죠.
현재 시점에서 바라보면 아쉬움이 많습니다.
'개발 Note > 값 중심의 언어' 카테고리의 다른 글
| 감명 깊었던 programming language principles 5- 값 중심의 언어 - 메모리 주소 값 (0) | 2014.12.11 |
|---|---|
| 감명 깊었던 programming language principles 5- 값 중심의 언어 (1) | 2014.12.10 |
| 감명 깊었던 programming language principles 4- 기계 중심 언어-메모리 관리 (0) | 2014.12.04 |
| 감명 깊었던 programming language principles 4- 기계 중심 언어 (0) | 2014.12.03 |
| 감명 깊었던 programming language principles 3- 모양과 뜻 (0) | 2014.11.26 |
(R1) 
(R2) 
(R3) 
(R4)
(R5) 
(R6)
(R7) 
(R8)
(R9) 
(R10)
(R11) 
(R12)
의 증명을 위의 증명규칙으로 만들면 아래의 나무 구조가 됩니다. 
의 f는 모두 참인가? 반대로, 참인 식들은 모두 위의 증명규칙들을 통해서 
는 유한하고 비어있지 않은 상태들의 집합
는 유한하고 비어있지 않은 기호와 알파벳들의 집합
는 비어있음을 알려주는 기호 (테이프 위에서 유일하게 무한하게 나타날 수 있는 기호)
는 입력가능한 기호들의 집합
는 초기상태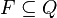
는 최종상태, 또는 수락 상태
는 부분함수