1. 컴퓨터는 프로그래밍 언어에서 시작되었다!!.
대부분 프로그래밍 언어란 무엇인가요? 라는 질문에, 컴퓨터에서 돌아가기 위해 만들어진 언어 라고 대답할 것입니다.
맞는 예기죠. 당연한 것이죠.
그런데 컴퓨터는 왜 만들어 졌나요? 라고 질문한다면.... 어떻게 대답해야 할까요?
필요에 의해서? 그럼 무슨 필요에 의해서 일까요?
이 질문에 답하기 위해서는 컴퓨터의 시초로 거슬러 올라가서 한계단 한계단 밟으면서 컴퓨터 사이언스 역사를 살펴봐야 합니다.
결론 부터 예기하고 이것 저것 살펴보죠.
"컴퓨터는 프로그래밍 언어를 구동시키기 위해 만들어 졌습니다."
즉, 컴퓨터 보다 프로그래밍 언어가 먼저 만들어졌고, 이를 확인하고 증명하는 과정에서 컴퓨터가 만들어 졌습니다.
정말이냐구요?
자.간략히 프로그래밍 언어의 시초에 대해서 언급하겠습니다.
1920년대 당대에 위대한 수학자 중 하나였던 힐베르트(다비트 힐베르트) 할아버지가,"모든 참인 명제를 증명할 수 있는 공리계가 있다" 라는 가설을 만들었습니다.
당시 힐베르트는 기하학(유클리드 기하학)을 공리화 하였고, 공간을 정의하여 함수해석학의 기초를 닦았다고 합니다. 아마 이런 과정에서 힐베르트는 위와 같이 모든 것은 증명할 수 있는 어떤것이 있다는 가설을 세우게 되었습니다.
이 의미는 간단하게 "모든 수학적 명제는 참인지 거짓인지 자동으로 계산 할 수 있다."라는 것이었습니다.
1930년대 초 쿠르트 괴델이 불완정성 정리를 증명하면서, 수학의 형식화가 태생적으로 한계가 있다는 것을 증명 했습니다. <불완전성의 원리>
1936년 쿠르트 괴델의 증명을 보고 , 앨런 튜링은 다른 형식으로 이를 증명하게 됩니다.
이때 나온게 튜링 머신이라는 것인데, 초보적인 컴퓨터라고 이해하는 사람들이 있는데, 초보적인 기계어라고 이해 하는것이 더 맞을 것입니다.
튜링 머신 자체가 실제로 존제하는 기계가 아니라 이론이었고, 표현 자체가 기호와 수학에 의해 정리되어있기 때문입니다.<튜링머신>
이와 비슷한 시기인 1930년대 알론조 처치가 람다 대수의 형식을 제안하였습니다.<람다 대수>
람다대수는 계산이론, 언어학 등에 중요한 역할을 하고, 프로그래밍 언어 이론의 발전에 토대가 되었고, 리스프, 함수형 프로그래밍 언어는 람다 대수로부터 직접적인 영향을 받아 탄생했으며, 단순 타입 람다 대수는 현대 프로그래밍 언어의 타입 이론의 기초가 되었습니다.
이와 같이 1930년대가 Computer라는 정의가 처음 시작되던 시기인데, 힐베르트의 가설이 불가능 하다는 것을 증명하기 위해서 고안된것이 컴퓨터의 시초이고 프로그래밍 언어의 시초입니다.
힐베르트의 가설은 참, 매력적인데, "모든 참인 명제를 증명할 수 있는 공리계가 있다" 는 것이 만약 참으로 증명되었다면, 현재의 컴퓨터는 아마도 더 완벽한 것이었을 거라고 생각됩니다.
그러나 아이러니하게도, 우리는 컴퓨터는 이 명제가 틀렸다는 증명을 위해 고안되었습니다.
(이것이 불행일까요? 인간이 불완전 하다는 것을 생각해본다면, 뭐 나쁘진 않다고 봅니다. 오히려 발전의 가능성이 더 있다고 생각해 볼수 있겠죠... 뭔가 철학적인 ...)
때문에, 이런 거짓인 명제를 포함한 채로 Computer science 와 Computer engineering 은 발전해왔고, 그래서 지금도 여전히 불완전 한것은 맞습니다.
아무튼, 튜링이 튜링머신이라는 가상의 기계를 만들고, 그 기계가 동작하는 방식을 설명했는데, 기계라고 표현했지만, 기계적 장치는 없고, 이는 현재 프로그래밍 언어가 컴퓨터를 동작시키는 방식을 설명한 것이었습니다..
(지금의 CPU,RAM, 출력장치 등의 기본 개념이 이때 제안 되었다고 봐도 됩니다.)
이런 일련의 사건들을 보면, 컴퓨터가 없던 시절에 프로그래밍 언어의 시초가 되는 튜링 머신이나, 람다 대수식 등이 등장했고, 이후 이 튜링머신이나 람다 대수를 동작시켜볼 수 있는 장치로 컴퓨터가 고안되고 발전 했다 라고 할 수 있습니다.(실제로 그랬구요.)
개인적으로는 별로 생각해보지 않았던 부분이고, 누군가 질문했다면, "글쎄요.." 라고 대답 했을 것 같았는데, 막상 여기저기 찾아보고, 조사해보니, 프로그래밍 언어와 컴퓨터라는 것에 대해서 새로운 시각을 갖게 되는 것 같습니다.
힐베르트의 가설이 잘못된 것임을 증명한, 괴델(리커시브 함수), 튜링( 정지 문제), 처치( 결정 불가능 문제) 는 본질적으로 같은 것이라는 사실도 재미 있습니다.
다시 한번, 컴퓨터는 왜 만들어 졌나요? 라고 질문 한다면,
이제 우리는 프로그래밍 언어를 돌리기 위해서 컴퓨터가 만들어 졌어요.. 라고 답할 수 있습니다.
이러면 날 수 있을 꺼라 생각 했었던 시절.
<< Appendix >>
튜링기계
"...무한한 저장공간은 무한한 길이의 테이프로 나타나는데 이 테이프는 하나의 기호를 인쇄할 수 있는 크기의 정사각형들로 쪼개져있다. 언제든지 기계속에는 하나의 기호가 들어가있고 이를 "읽힌 기호"라고 한다. 이 기계는 "읽힌 기호"를 바꿀 수 있는데 그 기계의 행동은 오직 읽힌 기호만이 결정한다. 테이프는 앞뒤로 움직일 수 있어서 모든 기호들은 적어도 한번씩은 기계에게 읽힐 것이다" - 튜링 ,1948, p.61 |
1935년 봄, 케임브리지 킹스 칼리지의 젊은 박사 과정 학생이었던 튜링은 한 과제에 직면했다. 그는 논리학자 뉴먼의 강의에 자극을 받았으며, 결정 문제에 대한 괴델의 연구에 대해 알게되었다. 뉴먼은 '기계적'이라는 단어를 사용했으며, 1955년 튜링의 부고에 뉴먼은 다음과 같이 기술 했습니다.
" '[기계적] 과정이란 무엇인가?'라는 질문에 튜링은 '기계로 할 수 있는 것' 이라는 답을 내 놓았다." - Gandy, p.74 |
테이프 튜링기계

 는 유한하고 비어있지 않은 상태들의 집합
는 유한하고 비어있지 않은 상태들의 집합 는 유한하고 비어있지 않은 기호와 알파벳들의 집합
는 유한하고 비어있지 않은 기호와 알파벳들의 집합 는 비어있음을 알려주는 기호 (테이프 위에서 유일하게 무한하게 나타날 수 있는 기호)
는 비어있음을 알려주는 기호 (테이프 위에서 유일하게 무한하게 나타날 수 있는 기호) 는 입력가능한 기호들의 집합
는 입력가능한 기호들의 집합 는 초기상태
는 초기상태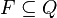 는 최종상태, 또는 수락 상태
는 최종상태, 또는 수락 상태 는 부분함수
는 부분함수
람다 대수 Lambda Calculus
- 알파-변환(α-conversion): 속박 변수를 바꿈
- 베타-축약(β-reduction): 식의 인수에 함수를 적용
- 에타-변환(η-conversion): 외연성을 통해 축약 (겉으로 보이는 행동이 같은 함수는 동일 함수로 간주함)
'개발 Note > 값 중심의 언어' 카테고리의 다른 글
| 감명 깊었던 programming language principles 4- 기계 중심 언어- 타입시스템 (1) | 2014.12.09 |
|---|---|
| 감명 깊었던 programming language principles 4- 기계 중심 언어-메모리 관리 (0) | 2014.12.04 |
| 감명 깊었던 programming language principles 4- 기계 중심 언어 (0) | 2014.12.03 |
| 감명 깊었던 programming language principles 3- 모양과 뜻 (0) | 2014.11.26 |
| 감명 깊었던 programming language principles 2-기본기 (4) | 2014.11.12 |


